Misure ed errori
A. Costantini | (la videolezione) Nessuna grandezza fisica può essere
misurata con completa certezza, di conseguenza la parola "errore" assume il significato di incertezza da associare alla misura. L’errore è qualcosa che si può ridurre, mai eliminare completamente:
quindi esiste per ogni misura. Ma come si effettuano le misure? Di solito si utilizzano strumenti di
misura, in grado di fornire dati più precisi delle stime “a occhio” (comunque largamente usate dai
fisici per farsi un’idea rapida dei fenomeni). Esiste una grandissima varietà di strumenti, dal righello
all’orologio atomico, ma tutti condividono alcune caratteristiche fondamentali, che elenchiamo qui
di seguito:
- Portata: è l’intervallo massimo di valori (della grandezza fisica) che lo strumento riesce a misurare. Per esempio, la portata di un righello da 20 cm è proprio 20 cm. Un normale orologio a lancette ha una portata di 12 ore.
- Prontezza: è la rapidità di risposta dello strumento. Un termometro a mercurio impiega circa otto minuti a misurare la temperatura del corpo umano, mentre un moderno termometro digitale può fare la stessa cosa in meno di cinque secondi.
- Sensibilità: è la più piccola variazione della grandezza apprezzabile dallo strumento, ovvero la più piccola variazione della sollecitazione che produce una variazione nella risposta dello strumento. Per esempio, un normale righello ha sensibilità 1 mm, cioè la più piccola divisione apprezzabile sulla scala dello strumento.
- Accuratezza: spesso confusa con la precisione, indica di quanto il valore indicato dallo strumento si discosta dal valore vero della grandezza misurata. In altri termini, la caratteristica di uno strumento di fornire misure vicine al valore vero della grandezza misurata viene detta accuratezza.
Tipologia degli errori
In generale, un errore può essere
- accidentale: dovuto alla scarsa abilità di chi misura oppure ai limiti dello strumento;
- casuale: generato da fluttuazioni imprevedibili;
- sistematico: dovuto a malfunzionamento dello strumento di misura o a cause esterne di cui non si è tenuto conto.
Un esempio di errore accidentale è quello che si verifica quando misuriamo con un normale metro a nastro l’altezza di un muro, tenendo però il nastro in posizione obliqua. In tal caso è chiaro che il valore ottenuto è superiore all’altezza effettiva del muro. Un esempio di errore sistematico è invece quello che si ottiene misurando un intervallo di tempo con un orologio che “va avanti”. Tutti i valori in questo caso ottenuti saranno più piccoli di quelli “veri”. L’errore sistematico è molto più pericoloso di quello accidentale, perché in alcuni casi è quasi impossibile accorgersi della sua presenza. Un orologio che va avanti si può correggere solo usandone un altro che sia corretto: ma come possiamo accertarci che anche il secondo non vada avanti (o indietro)? L’errore sistematico è, con quello casuale, l’avversario più difficile da affrontare, ma qui ci occuperemo quasi esclusivamente di misure facili: il seguito di questo post riguarderà quindi solo l’errore accidentale. Passiamo a qualche esempio concreto. Cominceremo con le misure di lunghezza, perché sono familiari e abbastanza semplici da eseguire. Consideriamo la situazione rappresentata nel disegno qui in basso.
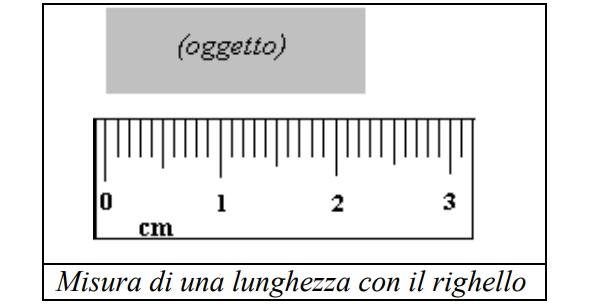La lunghezza dell’oggetto è compresa fra 2,2 e
2,3 cm: non è possibile dire di più se non si dispone di
uno strumento con divisioni più piccole (cioè uno
strumento dotato di maggiore sensibilità). Quello che
allora si deve scrivere per la lunghezza L dell’oggetto è
L = (2,25 ± 0,05) cm. Il motivo è che ci si mette a metà
tra 2,2 e 2,3 e si sceglie l’intervallo in modo da beccare
al minimo 2,2 e al massimo 2,3; questo è il significato
del simbolo ±. La quantità che segue tale simbolo si chiama errore assoluto. Se siamo nel caso in
cui si possa trascurare l’errore sistematico, allora l’errore assoluto è sempre uguale a metà della
sensibilità dello strumento di misura che stiamo usando. L’errore assoluto diviso per il valore della grandezza prende il nome di errore relativo e, trattandosi del rapporto di due quantità
espresse nelle stesse unità, non ha unità di misura: è una grandezza adimensionale.
L’errore relativo è più importante dell’assoluto, perché esprime il grado di precisione di una
misura: un esempio aiuterà a chiarire il concetto.
Misura 1: supponiamo di misurare un banco di scuola con un metro a nastro, trovando per la lunghezza il valore a = (750,0 ± 0,5) mm. L’errore assoluto è Δa = 0,5 mm e l’errore relativo è Δa/a = 0,5/750 = 0,00066.
Misura 2: misuriamo, con un fascio laser e uno specchio, la distanza tra il punto in cui ci troviamo e un punto della superficie lunare2 . In questo caso un valore attendibile è D = 384456 km, con un errore assoluto ΔD = 50 cm, cioè 0.0005 km. Confrontiamo le misure di a e D: l’errore assoluto su a è mille volte più piccolo di quello su D, ma nessuno direbbe che la misura di a è più precisa. Il motivo è che D è molto più grande di a! Infatti D è misurato assai meglio di a, perché il suo errore relativo è ER(D) = ΔD/D = = 0,0005/384456 = 0,0000000013, un numero cinquecentomila volte più piccolo di ER(a). Da quanto abbiamo visto, un errore relativo più piccolo corrisponde a una precisione maggiore.
L’errore percentuale, invece, è una variante dell’errore relativo: si ottiene infatti da esso moltiplicandolo per 100. L’errore relativo su a dell’esempio precedente, 0.00066, corrisponde a un errore percentuale E%(a) = ER(a)·100 = 0,06 % .
Propagazione degli errori
Capita molto spesso che una misura debba essere manipolata per ricavare altri risultati. Per esempio, non si misura mai direttamente la superficie di un cerchio, ma piuttosto se ne misura il diametro. lo si divide per 2, si eleva al quadrato e infine si moltiplica per π.
A questo punto sorge il problema: conoscendo l’errore su D, cioè noto D ± ΔD, come si può valutare quello risultante su S?
Per ogni operazione esistono delle regole, che diamo senza dimostrazione:
SOMMA : date le grandezze a ±Δa, b ± Δb, l’errore assoluto sulla somma a + b è la somma degli errori assoluti. Quindi EA(a+b) = Δa + Δb.
DIFFERENZA : date le grandezze a ±Δa, b ± Δb, l’errore assoluto sulla differenza a - b è ancora la somma degli errori assoluti. Quindi EA(a-b) = Δa + Δb.
PRODOTTO: date le grandezze a ±Δa, b ± Δb, l’errore relativo sul prodotto a · b è la somma degli errori relativi. Quindi ER(a·b) = ER(a) + ER(b) = Δa/a + Δb/b.
QUOZIENTE: date le grandezze a ±Δa, b ± Δb, l’errore relativo sul quoziente a · b è la somma degli errori relativi. Quindi ER(a:b) = ER(a) + ER(b) = Δa/a + Δb/b.
Le cifre significative e l’arrotondamento
Torniamo alla superficie del cerchio e supponiamo di aver trovato S = (200,96 ± 2,512) cmq . Così è scritto male però: il numero di cifre dopo la virgola deve essere uguale per la misura e per l’errore assoluto. Potremmo allora scrivere (200,960 ± 2,512) cmq ; però l’errore assoluto supera i 2 cmq , quindi non ha molto senso tenersi tre cifre dopo la virgola, che potrebbero essere tutte sbagliate! In questi casi la regola è di tenere una cifra in più di quella dove “comincia” l’errore: per il nostro esempio l’errore è sulle unità (la cifra subito prima della virgola), pertanto sembrerebbe giusto scrivere (200,9 ± 2,5) cmq . Ma non va ancora bene, perché 200,96 è più vicino a 201 che a 200,9: si introduce così il concetto di arrotondamento. Nel nostro caso la scrittura più corretta è S = (201,0 ± 2,5) cmq [lo zero dopo il 201 è necessario se si vuole che la misura e l’errore assoluto abbiano lo stesso numero di cifre dopo la virgola]. Nell’arrotondare un numero troncandone le cifre occorre tener presente quanto segue: - se la cifra da troncare è compresa fra 0 e 4: il numero che la precede resta immutato - se la cifra da troncare è compresa fra 5 e 9: il numero che la precede viene aumentato di 1 ESEMPIO: il numero 2,36942 si scrive
- 2 arrotondato senza cifre decimali
- 2,4 arrotondato alla prima cifra decimale
- 2,37 arrotondato alla seconda cifra decimale
- 2,369 arrotondato alla terza cifra decimale
- 2,3694 arrotondato alla quarta cifra decimale.
- Portata: è l’intervallo massimo di valori (della grandezza fisica) che lo strumento riesce a misurare. Per esempio, la portata di un righello da 20 cm è proprio 20 cm. Un normale orologio a lancette ha una portata di 12 ore.
- Prontezza: è la rapidità di risposta dello strumento. Un termometro a mercurio impiega circa otto minuti a misurare la temperatura del corpo umano, mentre un moderno termometro digitale può fare la stessa cosa in meno di cinque secondi.
- Sensibilità: è la più piccola variazione della grandezza apprezzabile dallo strumento, ovvero la più piccola variazione della sollecitazione che produce una variazione nella risposta dello strumento. Per esempio, un normale righello ha sensibilità 1 mm, cioè la più piccola divisione apprezzabile sulla scala dello strumento.
- Accuratezza: spesso confusa con la precisione, indica di quanto il valore indicato dallo strumento si discosta dal valore vero della grandezza misurata. In altri termini, la caratteristica di uno strumento di fornire misure vicine al valore vero della grandezza misurata viene detta accuratezza.
Tipologia degli errori
In generale, un errore può essere
- accidentale: dovuto alla scarsa abilità di chi misura oppure ai limiti dello strumento;
- casuale: generato da fluttuazioni imprevedibili;
- sistematico: dovuto a malfunzionamento dello strumento di misura o a cause esterne di cui non si è tenuto conto.
Un esempio di errore accidentale è quello che si verifica quando misuriamo con un normale metro a nastro l’altezza di un muro, tenendo però il nastro in posizione obliqua. In tal caso è chiaro che il valore ottenuto è superiore all’altezza effettiva del muro. Un esempio di errore sistematico è invece quello che si ottiene misurando un intervallo di tempo con un orologio che “va avanti”. Tutti i valori in questo caso ottenuti saranno più piccoli di quelli “veri”. L’errore sistematico è molto più pericoloso di quello accidentale, perché in alcuni casi è quasi impossibile accorgersi della sua presenza. Un orologio che va avanti si può correggere solo usandone un altro che sia corretto: ma come possiamo accertarci che anche il secondo non vada avanti (o indietro)? L’errore sistematico è, con quello casuale, l’avversario più difficile da affrontare, ma qui ci occuperemo quasi esclusivamente di misure facili: il seguito di questo post riguarderà quindi solo l’errore accidentale. Passiamo a qualche esempio concreto. Cominceremo con le misure di lunghezza, perché sono familiari e abbastanza semplici da eseguire. Consideriamo la situazione rappresentata nel disegno qui in basso.
Misura 1: supponiamo di misurare un banco di scuola con un metro a nastro, trovando per la lunghezza il valore a = (750,0 ± 0,5) mm. L’errore assoluto è Δa = 0,5 mm e l’errore relativo è Δa/a = 0,5/750 = 0,00066.
Misura 2: misuriamo, con un fascio laser e uno specchio, la distanza tra il punto in cui ci troviamo e un punto della superficie lunare2 . In questo caso un valore attendibile è D = 384456 km, con un errore assoluto ΔD = 50 cm, cioè 0.0005 km. Confrontiamo le misure di a e D: l’errore assoluto su a è mille volte più piccolo di quello su D, ma nessuno direbbe che la misura di a è più precisa. Il motivo è che D è molto più grande di a! Infatti D è misurato assai meglio di a, perché il suo errore relativo è ER(D) = ΔD/D = = 0,0005/384456 = 0,0000000013, un numero cinquecentomila volte più piccolo di ER(a). Da quanto abbiamo visto, un errore relativo più piccolo corrisponde a una precisione maggiore.
L’errore percentuale, invece, è una variante dell’errore relativo: si ottiene infatti da esso moltiplicandolo per 100. L’errore relativo su a dell’esempio precedente, 0.00066, corrisponde a un errore percentuale E%(a) = ER(a)·100 = 0,06 % .
Propagazione degli errori
Capita molto spesso che una misura debba essere manipolata per ricavare altri risultati. Per esempio, non si misura mai direttamente la superficie di un cerchio, ma piuttosto se ne misura il diametro. lo si divide per 2, si eleva al quadrato e infine si moltiplica per π.
A questo punto sorge il problema: conoscendo l’errore su D, cioè noto D ± ΔD, come si può valutare quello risultante su S?
Per ogni operazione esistono delle regole, che diamo senza dimostrazione:
SOMMA : date le grandezze a ±Δa, b ± Δb, l’errore assoluto sulla somma a + b è la somma degli errori assoluti. Quindi EA(a+b) = Δa + Δb.
DIFFERENZA : date le grandezze a ±Δa, b ± Δb, l’errore assoluto sulla differenza a - b è ancora la somma degli errori assoluti. Quindi EA(a-b) = Δa + Δb.
PRODOTTO: date le grandezze a ±Δa, b ± Δb, l’errore relativo sul prodotto a · b è la somma degli errori relativi. Quindi ER(a·b) = ER(a) + ER(b) = Δa/a + Δb/b.
QUOZIENTE: date le grandezze a ±Δa, b ± Δb, l’errore relativo sul quoziente a · b è la somma degli errori relativi. Quindi ER(a:b) = ER(a) + ER(b) = Δa/a + Δb/b.
Le cifre significative e l’arrotondamento
Torniamo alla superficie del cerchio e supponiamo di aver trovato S = (200,96 ± 2,512) cmq . Così è scritto male però: il numero di cifre dopo la virgola deve essere uguale per la misura e per l’errore assoluto. Potremmo allora scrivere (200,960 ± 2,512) cmq ; però l’errore assoluto supera i 2 cmq , quindi non ha molto senso tenersi tre cifre dopo la virgola, che potrebbero essere tutte sbagliate! In questi casi la regola è di tenere una cifra in più di quella dove “comincia” l’errore: per il nostro esempio l’errore è sulle unità (la cifra subito prima della virgola), pertanto sembrerebbe giusto scrivere (200,9 ± 2,5) cmq . Ma non va ancora bene, perché 200,96 è più vicino a 201 che a 200,9: si introduce così il concetto di arrotondamento. Nel nostro caso la scrittura più corretta è S = (201,0 ± 2,5) cmq [lo zero dopo il 201 è necessario se si vuole che la misura e l’errore assoluto abbiano lo stesso numero di cifre dopo la virgola]. Nell’arrotondare un numero troncandone le cifre occorre tener presente quanto segue: - se la cifra da troncare è compresa fra 0 e 4: il numero che la precede resta immutato - se la cifra da troncare è compresa fra 5 e 9: il numero che la precede viene aumentato di 1 ESEMPIO: il numero 2,36942 si scrive
- 2 arrotondato senza cifre decimali
- 2,4 arrotondato alla prima cifra decimale
- 2,37 arrotondato alla seconda cifra decimale
- 2,369 arrotondato alla terza cifra decimale
- 2,3694 arrotondato alla quarta cifra decimale.
