Esercitazione sulle mappe di Karnaugh
1 Bisogna individuare il minor numero di gruppi (che copre tutti gli 1 della mappa).
2 Ciascun gruppo deve contenere il maggior numero di 1 adiacenti (il numero di 1 che costituisce un gruppo deve formare una potenza del 2, si scelgono perciò gruppi da due 1, da quattro, da otto, etc..).
3 Sono considerabili adiacenti le caselle di estremità.
4 Eventuali 1 isolati costituiscono un gruppo e debbono essere riportati integralmente.
5 Da ogni gruppo si estrae un termine che contiene le variabili di ingresso che non variano passando da una casella all’altra del raggruppamento stesso, ciascuna variabile sarà in forma vera o negata a secondo se vale 1 o 0 nel raggruppamento.
6 La funzione logica minimizzata sarà data dalla OR dei termini estratti dalla mappa.
Ad esempio:
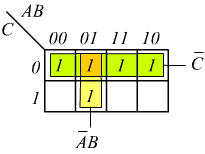
Come si nota il minimo numero di gruppi è due, ciascun gruppo contiene tanti 1 sempre in ragione delle potenze del 2 (cioè 4 e 2 uno) nel primo gruppo orizzontale passando da una casella all’altra l ’unica variabile che non cambia è la C che rimane impostata a 0 per cui verrà estratta come termine C. Nel gruppo verticale passando da una casella all’altra le variabili che non cambiano sono la A che rimane impostata a 0 (A) e la B che rimane impostata a 1 (B); verrà dunque estratto il termine AB; in definitiva la funzione semplificata sarà:
![]()

