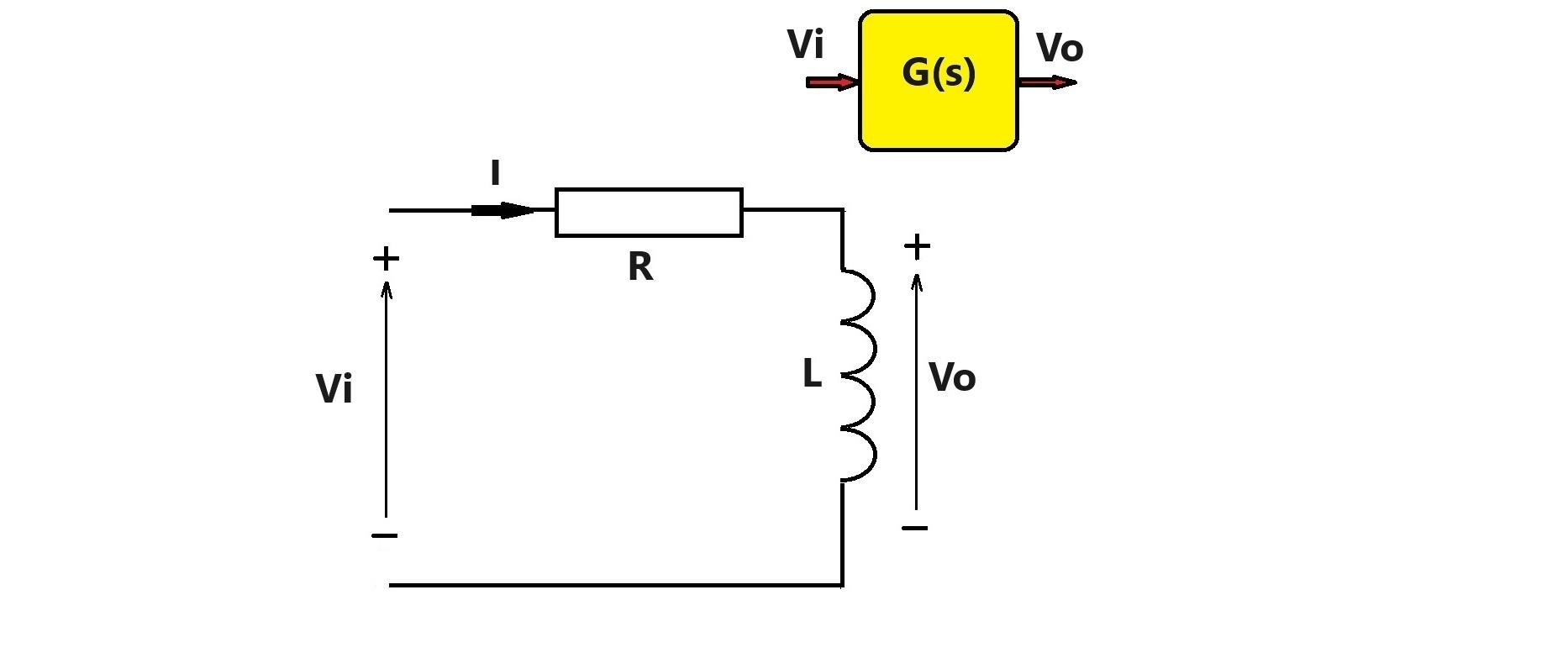
Funzione di trasferimento di un RL

A. Costantini | (la videolezione) Determiniamo, a titolo di esempio, la funzione di trasferimento di un banale circuito RL (resistenza e induttanza). Immaginiamo di considerare come ingresso la tensione Vi del circuito e come uscita la tensione sui terminali dell’induttore. Sappiamo che la funzione di trasferimento “G(s)” è definita come rapporto tra l'uscita e l'ingresso di un sistema, nel dominio di Laplace. Applicando le leggi dell’elettrotecnica, vediamo com’è possibile ricavare la funzione di trasferimento di questo banale circuito. Osserviamo che, conoscendo la corrente, è possibile determinare la tensione di uscita Vo con la legge di Ohm:

Vo = Z2 I

Dove Z2 è l'impedenza dell'induttore nel dominio di Laplace. Ricordiamo che l’impedenza dell’induttore nel dominio di Laplace si scrive come:

Z2 = sL

mentre l'impedenza della resistore Z1 coincide con resistenza R. In sostanza, volendo determinare la tensione di uscita (Vo), occorrerà moltiplicare l'impedenza Z2 per la corrente. (legge di Ohm nel dominio di Laplace). Sostituendo in Z2 il prodotto sL otteniamo:

Vo = sL I

Per ricavare la funzione di trasferimento, ora, c’è bisogno di far comparire la “Vi” in questa espressione. Per far questo, è possibile calcolare la corrente e scrivere che la corrente è uguale alla tensione in ingresso Vi divisa per l’impedenza totale del circuito . Trattandosi di due impedenze in serie, l’impedenza totale sarà:

Z = Z1 + Z2

In definitiva la corrente sarà:

I = Vi / Z = Vi /(Z1+Z2)

Sostituendo alle due impedenze le rispettive espressioni (quelle scritte sopra) avremo:

I = Vi /(R +sL)

dove R più sL è l'impedenza del circuito nel domino di Laplace. Sostituiamo al posto della corrente l’espressione appena ricavata si ha:

Vo = sL I = sL Vi /(R+sL)

Cioè l'espressione della tensione di uscita di questo circuito.

Come già detto, la funzione di trasferimento “G(s)” è semplicemente il rapporto, nel domino di Laplace, di Vo e Vi. Se nelle espressioni di sopra si divide primo e secondo membro per Vi, al primo membro si ottiene proprio la funzione di trasferimento:

Vo / Vi = sL /(R+sL)

G(s) = sL /(R+sL)