Segnali nel dominio della frequenza

(la videolezione) Quando pensiamo a un segnale elettrico, lo immaginiamo spesso come una grandezza elettrica (tensione o corrente) che cambia nel tempo. Questo è il dominio del tempo, dove si analizzano l'ampiezza, la fase e la forma del segnale in relazione al tempo. Tuttavia, per comprendere appieno la natura di molti segnali, in particolare quelli di una certa complessità, è fondamentale analizzarli anche nel dominio della frequenza. Questo approccio ci permette di scomporre un segnale nelle sue componenti sinusoidali più semplici, rivelando quali frequenze lo compongono e con quale intensità.

La chiave per passare dal dominio del tempo al dominio della frequenza è la trasformata di Fourier. Questo strumento matematico, ideato da Joseph Fourier, dimostra che ogni segnale periodico può essere rappresentato come una somma di segnali sinusoidali (seno e coseno) a diverse frequenze. Ognuna di questi segnali ha una propria ampiezza e una fase. In altre parole, la trasformata di Fourier "svela" lo spettro di frequenze di un segnale.

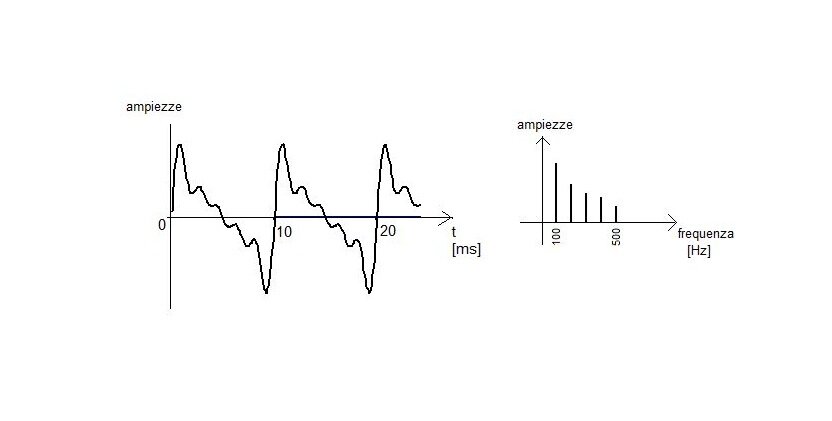
L'analisi nel dominio della frequenza produce uno spettro di frequenza, che è una rappresentazione grafica del segnale. Sull'asse orizzontale troviamo la frequenza (f), e sull'asse verticale l'ampiezza (o la potenza) di ciascuna componente di frequenza. I segnali semplici, come una singola sinusoide, mostrano un picco netto a una sola frequenza. I segnali complessi, come la voce umana o la musica, hanno uno spettro più ricco e distribuito.

Un concetto correlato è la banda passante di un segnale, che è l'intervallo di frequenze in cui l'energia (o potenza) del segnale è significativa. È un parametro cruciale per i sistemi di comunicazione: i canali di trasmissione, come i cavi coassiali o le onde radio, devono avere una banda passante sufficientemente ampia da non distorcere il segnale che trasportano.

L'analisi dei segnali nel dominio della frequenza offre numerosi vantaggi:

Identificazione del rumore: Il rumore elettrico, spesso a frequenze specifiche (es. rumore a 50/60 Hz dalla rete elettrica), può essere facilmente individuato e filtrato.

Progettazione di filtri: Permette di progettare filtri (passa-alto, passa-basso, passa-banda) che eliminano o attenuano selettivamente le frequenze indesiderate. Ad esempio, in un'applicazione audio, si può filtrare il rumore di fondo a bassa frequenza.

Modulazione: Nelle telecomunicazioni, la modulazione (es. AM, FM) sfrutta il dominio della frequenza per spostare il segnale a frequenze portanti più alte, rendendolo adatto alla trasmissione radio.

Compressione dei dati: Algoritmi di compressione come JPEG e MP3 operano sul principio della trasformata di Fourier, scartando le frequenze meno importanti per l'orecchio o l'occhio umano, riducendo così la dimensione del file.